RESIDUAL STRESS CAUSED BY SHRINKAGE OF THERMOSET POLYMERS
This post is based on the discussion of its topic by J. Bicerano, Prediction of Polymer Properties, third edition, Marcel Dekker, New York, 2002, as supplemented by the additional information and literature cited below.
The coefficient of linear thermal expansion β simply equals one third of the coefficient of volumetric thermal expansion α for an isotropic (non-oriented) material:
![]()
Thermoset polymers are often used in intimate contact with materials possessing much lower coefficients of linear thermal expansion. The following are some examples:
- A thermoset polymer coating on the surface of a metal or a ceramic.
- A thermoset polymer adhesive between two metal surfaces, between two ceramic surfaces, or between a metal surface and a ceramic surface.
- A thermoset polymer matrix containing and serving as a binder to high-modulus (such as carbon, glass, or aramid) fibers, in a fiber-reinforced composite.
The following table, adapted from the website of the NDT Resource Center, summarizes the coefficients of linear thermal expansion β of some common materials at room temperature.

A more comprehensive online discussion of the coefficient of linear thermal expansion can be found on the SpecialChem website
Residual stress can build up in all such systems because of the differences in the magnitude of the shrinkage caused by the different volumetric responses of the thermoset polymer and the other material(s) to changes in temperature. The thermoset polymer is prevented, because it is in intimate contact with the metal and/or ceramic surface(s), from shrinking as much as it would if it had been by itself, creating residual stress.
The curing of a thermoset polymer coating, adhesive, or matrix in intimate contact with metal and/or ceramic surface(s) is a common process that introduces residual stresses. The magnitude of the residual stress typically reflects the balance between the driving force to produce the residual stress due to differential shrinkage upon cooling and the temperature-dependent capacity to relax this stress. The worst such effects usually occur as the temperature drops below the glass transition temperature (Tg) of the thermoset polymer during curing (as Tg increases rapidly after gelation) or after curing (while the fabricated article is being cooled to room temperature).
As described in the open access manuscript by D.U. Shah and P.J. Schubel, Evaluation of Cure Shrinkage Measurement Techniques for Thermosetting Resins, Polymer Testing (2010) and illustrated in the image (reproduced from this manuscript) shown below this paragraph, the decrease of the specific volume during the curing process can usually be described as occurring in three distinct regions. The resin is uncured and behaves as a viscous fluid, and the mobile liquid monomer molecules can be considered as discrete chemical entities, in Region I. The monomer molecules react exothermically to first undergo chain formation and linear growth through branching (polymerization) and then form cross-links so that a rigid continuous three-dimensional molecular network is formed, in Region II which denotes the curing stage. Region III marks the end of the curing process.

The following equation provides a crude approximation, based on a general theory for the elastic interactions in a composite plate of layers with different relaxed planar dimension, for the residual stress:
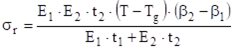
The following notation is used in this equation:
- σr: Residual stress.
- E1 and E2: Tensile (Young’s) elastic moduli of the thermoset (Material 1) and the substrate (Material 2).
- t1 and t2: Thicknesses of the layers of thermoset and substrate.
- (β2 – β1): Difference between the coefficients of linear thermal expansion (β2<β1, and in many cases β2<<β1).
- (T - Tg): Difference between the use temperature (T) and the glass transition temperature of the thermoset (Tg); with (T - Tg)<0, and in many cases (T - Tg)<<0.
The increasingly more accurate estimation of such residual stresses and the development of methods for their reduction is an active area of materials research and development. An example from the leading edge of such research will be provided below.
Prof. Dr. J. G. E. M. Fraaije, of Leiden University, and also the founder of CULGI which develops materials modeling and simulation software, provided the example described in the remainder of this post. Dr. J.-W. Handgraaf, Chief Application Scientist at CULGI, is also acknowledged for his contribution to the work summarized below. See the post titled SOFTWARE FOR MATERIALS MODELING AND SIMULATION (created 29 November 2018) for a review of the CULGI software.
Dental restorative materials are highly cross-linked polymer networks synthesized by free radical polymerization of multifunctional base monomers. The volumetric polymerization shrinkage of such materials can destroy the balance between the filling and tooth structure and eventually cause micro-leakage. Proper understanding and control of shrinkage is essential for the development of new formulations to be used as dental materials. The shrinkage stress of composite resins and resin cements used in dentistry was reviewed in a recent open access article by Soares et al. from which the images below were reproduced.

A multiscale modeling protocol is being used with CULGI software to model the highly cross-linked polymer networks in studying volumetric polymerization shrinkage in dental materials. Coarse-grained models of the base monomers are developed. Mesoscopic models of the system containing the proper fractions of all monomers are prepared. Dissipative particle dynamics (DPD) simulations are then performed to equilibrate the system. Free radical polymerization reactions are activated within the DPD simulations, using the reactions plugin of the software to generate a realistic polymer network. The generated network is further equilibrated within the coarse-grained domain and then transformed into an atomistic detailed structure using a mapper that takes as input the mesoscopic morphology and uses Monte Carlo techniques to generate the atomistic structure. Molecular Dynamics simulations of the atomistic structure are then performed at constant pressure and temperature. Volumetric shrinkage during the gelation process is estimated from comparison of the predicted densities of the monomeric system and the network system. The predicted amounts of shrinkage of networks of methyl acrylate/acrylic acid and tetramethylolpropane were found to be in good agreement with experimental data. The protocol is now being used in the development of new dental material formulations. Images cannot be shown due to the confidentiality of the results.
